Leonhard Euler was born in Switzerland 312 years ago and at the age of 13 he attended the University of Basel where he received a Master’s Degree in Philosophy. The Euler family were also very close friends with the Bernoulli family. It was Johann Bernoulli who discovered Leonhard’s incredible talent for mathematics.
Euler was blind in one eye by 1730. By 1755 he had produced over 50 papers whilst being partially sighted. By 1771 he became blind in both eyes, but this did not stop him following his passion by continuing to produce further papers on mathematics theory.
Leonhard Euler’s work made an impact in numerous areas of mathematics and is credited in the science and engineering disciplines for popularising modern notation and terminology. Below is a description of some of Euler’s theories and assumptions relating to engineering.
Euler’s Critical Loads
The critical load is the maximum load (in Newtons) that a column can bear while staying straight.
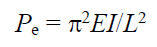
Where:
Pe = Euler buckling load (N)
E = Young’s modulus (Nm−1)
I = Second moment of area (m4)
L = Length of strut (m)
Euler’s Laws of Motion
50 years after Newton published his Laws of Motion, Euler expanded upon this to determine the point particle to rigid body motion.
Expanding from Newton’s initial law, Euler’s first law states that the Linear Momentum of a body P is equal to the product of the mass of the body m and the velocity of the centre mass vcm .
Euler then decided to develop another one of Newton’s Law of Motions from his findings from the previous law, however this law looks at the change of angular momentum known as L. L is seen to be a fixed point in an inertial reference frame often in the centre mass of the body, and is equal to the external moments of force acting on the body M at any given point.
Practical Applications for Learning About Euler’s Equations
TecQuipment offers a dedicated set of equipment for illustrating Euler’s theories in practical terms. Click on the links below to find out further details.
- To define Euler’s Critical Load use TecQuipment’s Euler Buckling Apparatus.